CONDUCTORS AND CAPACITORS
CONDUCTORS AND INSULATORS
All matter is made up of atoms. Atoms are made up of protons, neutrons and electrons. Protons and neutrons reside in an extremely tiny space inside the atom called the nucleus. Electrons keep moving outside the nucleus in some especial energy levels. (If you assume that the nucleus is the size of a sand grain then a small movie theater is the size of the atom!) The size of an electron is about one-tenth of the size of the nucleus.
The protons are positively charged, the electrons are negatively charged and the neutrons are neutral i.e they have no charge.
Since the protons and neutrons are oppositely charged therefore they attract each other due to coulomb’s law. (If they attract each other then why don’t they just collide and stick up with each other? The answer can be given from Quantum Mechanics which is beyond the scope of high school syllabus.Though some people try to give answers from Classical Physics but I don't think those answers are fully satisfactory.) It was explained in the article headed Coulomb's Law that this force of attraction follows an inverse square law. The farther away an electron is from the nucleus the lesser is the force of attraction due to the protons. There are some more reasons also that effect the attractive force on an electron in an atom but we do not need to worry about them here.
Those "outer" electrons which experience a feeble force due to the nucleus can leave the atom by acquiring energy from sources like heat, external electric field etc, and move out freely in the material. This acquisition of energy is the key idea here.
When an external electric field is applied it forces the free electrons to flow in one direction. This constitutes an electric current.
Note that even the inner electrons can leave the atom by acquiring energy but that will require a very large amount of energy. So under ordinary circumstances only the outer electrons leave the atom. For e.g the energy required to remove the last electron from the Lithium atom (which has three electrons in all) requires an energy of 5.390 eV.* The energy required to remove the second last electron is 75.622 eV and the energy required to remove the innermost electron is 122.427 eV.
*eV is the contraction for the term 'electron-volt'. An electron-volt is defined as the energy gathered by an electron in falling through a potential difference of
1 volt. 1 eV = 1.6 x 10 ^ (-19) Joule. Its a common unit of atomic physics.
One more thing. The energy required to break a nucleus apart is even larger than what is required to eject inner electrons from an atom. Hence under ordinary circumstances we do not have to worry about the nucleus or inner electrons.
Electrons of some materials require a large amount of energy to get “free” while electrons of some other materials can do so by acquiring even a small amount of energy. Materials belonging to the former category are known as insulators or dielectrics and materials belonging to the latter category are known as conductors. Obviously this means that conductors have a very large - virtually infinite - number of free electrons and insulators have a very small - virtually zero - amount of free electrons.
In other words conductors allow electrical current to flow through them and insulators do not allow electrical current to flow through them.
ELECTROSTATICS OF CONDUCTORS
Suppose I place some charge on a conductor. Question. How will that charge distribute itself (if it will distribute at all) on that conductor? One may guess that the charge will move. Yes but until when? Till eternity?
It is found experimentally that when a charge is placed on a conductor the flow of charge stops after sometime in fact almost instantaneously. Now that is only possible if the field inside the conductor goes to zero AND the horizontal component of electric field on the surface of the conductor becomes zero else the horizontal component will keep pushing the charge and thus the charge will keep on moving till eternity. (This latter statement implies that the electric field on the surface of the conductor is always perpendicular to the surface. ) But a zero E implies a zero value of dV. Hence the potential difference between any two points of the conductor becomes zero. Or in other words whenever a charge is placed on the conductor it distributes itself in such a way that the conductor becomes an equipotential surface. By “equipotential” I mean a surface that has equal potential throughout.
So the E inside a conductor is zero and V is throughout the same.
Now what about the charges? How does the placed charge behave?
Gauss’ theorem comes to our rescue.
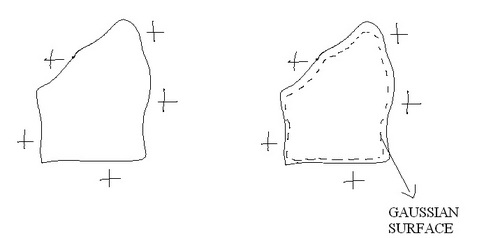
See the above diagram.
The gaussian surface is the boundary just inside the surface of the conductor shown by the dashed curve. Since the E inside is everywhere zero therefore the flux through this surface is obviously zero. But according to gauss' theorem flux = charge enclosed/epsilon naught. Therefore the charge enclosed by the conductor is zero!
Hence the charge given to the conductor distributes itself on the surface of the conductor only. It doesn’t goes inside.
See how useful is gauss’ theorem?
But until now I was speaking about only that charge that was given to the conductor. What if I place the conductor in an electric field? Well here also the charges (free electrons) of the conductor cease to move after some moments and so all the above results follow in a similar fashion. But now I can prove it to you that the charges have to stop after some time which I couldn't in the earlier case.
Suppose I place a neutral conductor in an electric field. Let's say the electric field goes from left to right.
The positive charge from the left region of the conductor goes to the right region and the negative charge goes from right to left. (Strictly speaking there is no "real movement" of the positive charge. Positive charge develops in those places which are deficient in negative charge. So electrically speaking a movement of negative charge from right to left is equivalent to the movement of positive charge from left to right.) This charge imbalance results in an extra electric field inside the conductor. But this field is in opposite direction to the external electric field hence the two fields tend to cancel each other. Since initially the external field was greater therefore it will continue to generate the flow of charge inside until the internal field becomes equal to the external field when they both destroy each other. Therefore the net electric field inside the conductor becomes zero.
Below I illustrate the above theory with the help of a diagram.
The gaussian surface is the boundary just inside the surface of the conductor shown by the dashed curve. Since the E inside is everywhere zero therefore the flux through this surface is obviously zero. But according to gauss' theorem flux = charge enclosed/epsilon naught. Therefore the charge enclosed by the conductor is zero!
Hence the charge given to the conductor distributes itself on the surface of the conductor only. It doesn’t goes inside.
See how useful is gauss’ theorem?
But until now I was speaking about only that charge that was given to the conductor. What if I place the conductor in an electric field? Well here also the charges (free electrons) of the conductor cease to move after some moments and so all the above results follow in a similar fashion. But now I can prove it to you that the charges have to stop after some time which I couldn't in the earlier case.
Suppose I place a neutral conductor in an electric field. Let's say the electric field goes from left to right.
The positive charge from the left region of the conductor goes to the right region and the negative charge goes from right to left. (Strictly speaking there is no "real movement" of the positive charge. Positive charge develops in those places which are deficient in negative charge. So electrically speaking a movement of negative charge from right to left is equivalent to the movement of positive charge from left to right.) This charge imbalance results in an extra electric field inside the conductor. But this field is in opposite direction to the external electric field hence the two fields tend to cancel each other. Since initially the external field was greater therefore it will continue to generate the flow of charge inside until the internal field becomes equal to the external field when they both destroy each other. Therefore the net electric field inside the conductor becomes zero.
Below I illustrate the above theory with the help of a diagram.
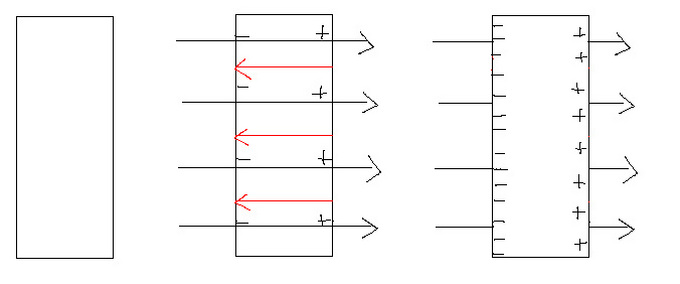
The above figure shows three snapshots of a cuboid shaped conductor. (One can chose any shaped and sized conductor. I chose cuboid only because it looks neat.) Only the cross-section is visible in the above diagram.
The leftmost figure refers to the state when the electric field is not switched on. The conductor is neutral throughout.
The middle figure represents the state just after the electric field is switched on. The electric field due to the internal charges is shown in red. This field grows until it becomes equal to the external field.
The rightmost figure shows the state when some time has elapsed after the external field was switched on. The field due to the internal charges has now grown to be equal to the external field and so the two have canceled each other.
PROPERTIES OF CONDUCTORS - A SUMMARY
Below I've summarized the important points discussed so far about conductors. Since I made no use of the shape and size of the conductor anywhere above therefore the properties discussed above and listed below apply to any kind of conductor.
- The electric field inside a conductor is always zero.
- The electric potential of a conductor throughout its volume is the same or the conductor is an equipotential surface.
- Any extra charge given to the conductor spreads on the surface only.
- The electric field at the surface of the conductor is always perpendicular to the surface.
|
|
UNIT OF CAPACITANCE
The unit of capacitance is coulomb/volt which is named as farad in honour of Michael Faraday. But farad is usually a large unit to deal therefore you may find units like micro farad (10 ^ -6 farad) or pico farad (10^ - 12) in common use in text books.
In the next article I will describe capacitors in more details.
|
|
For a brilliant discussion of Electrostatics and other such topics of Physics I recommend "Fundamentals of Physics" by Resnick, Walker and Halliday.
You may buy it by clicking on the link to the left. |