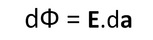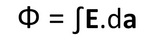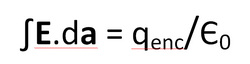GAUSS' THEOREM
AREA VECTOR
Although area is normally treated as a scalar quantity but sometimes its very useful to treat is as a vector. An area vector of a 2 dimensional object is defined as a vector whose length is proportional to the area of that object and whose direction is perpendicular to the plane of that area. But there are two perpendicular directions. So which one to chose?
If the object is closed three dimensionally (like a sphere) then the outward direction is taken as the positive direction and the inward direction as the negative one. If the object is open (like a thin page) then any direction can be arbitrarily chosen as positive or negative.
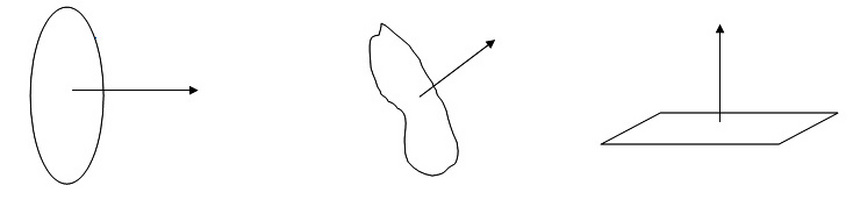
Area vector for a disc, an arbitrary 2D shape and a rectangle. Note all area vectors are drawn perpendicular to the surface. Though two such vectors are possible - one on each side of the surface - only one is shown in the above figure. Each vector can be taken as positive or negative according to the convenience of the user. Figure is not to scale.
Note - In the first paragraph I was talking about 2 D objects and in the second I mentioned sphere which is 3 D. So is this a contradiction?
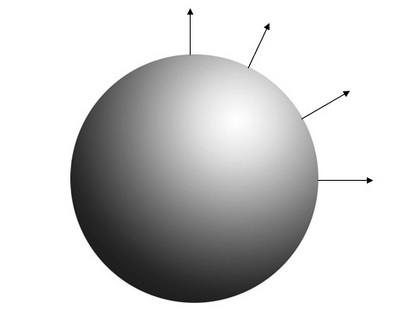
See, when I say a sphere then I don't mean that this entire sphere will have one area vector. This sphere can be imagined as to be consisting of many infinitesimally small 2 D areas. Look at the following figure to understand what I mean.
ELECTRIC FLUX
Now once the area vector has been defined I'm in a position to speak about flux.
Electric flux passing through an infinitesimally small body is defined as the dot product of area vector and electric field vector at the point where the body is placed. Its usually denoted by the letter phi of the Greek alphabet.
For a finite sized object the above equation should be integrated to get the desired results.
UNIT OF ELECTRIC FLUX
The unit of electrical flux in SI standard is volt metres (V m), or, equivalently, newton metres squared per coulomb (N m2 C−1).
Oil painting of Carl Friedrich Gauss (1777 - 1855) by G. Biermann
Carl Friedrich Gauss is known in the scientific community as the prince of mathematicians. Once when he was a kid his teacher asked the entire class to add all numbers from 1 to 100. Gauss immediately stood up and gave the correct answer. The teacher asked him to explain. He said he added numbers in pairs. He first added 1 with 100 and got 101. Then 2 with 99 and again got 101. Then 3 with 98 which again equals 101. There will be 50 such pairs. Hence the answer can be got by simply multiplying 50 with 101 which equals 5050.
His theorem of electromagnetism or Gauss' theorem is one of the basic principles of physics and is one of the four fundamental equations of Maxwell.
GAUSS' THEOREM
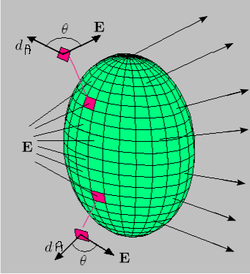
Gauss' theorem states that the total electrical flux passing through a closed three dimensional body is always equal to the charge enclosed by the body divided by epsilon naught.
One fourth world of electromagnetism is summed up in this single statement!
Now some details.
By a 'closed three dimensional body' I don't always mean a real body. Even where no body is present one can always assume an imaginary body and apply Gauss' theorem and it will work perfectly well.
The surface - whether real or imaginary - on which integration is performed in gauss' theorem is known as the gaussian surface.
Though Gauss' theorem is primarily intended to calculate electric flux but in symmetric situations it can be used to calculate electric field of different charge configurations. By 'symmetric situations' I mean those situations where electric field is known to be a constant on the entire surface where integration is being performed. Since E is a constant therefore it can be taken out of the integral sign and dA could be integrated and then E can be found.
This method has very powerful applications as will be discussed soon.
Now some details.
By a 'closed three dimensional body' I don't always mean a real body. Even where no body is present one can always assume an imaginary body and apply Gauss' theorem and it will work perfectly well.
The surface - whether real or imaginary - on which integration is performed in gauss' theorem is known as the gaussian surface.
Though Gauss' theorem is primarily intended to calculate electric flux but in symmetric situations it can be used to calculate electric field of different charge configurations. By 'symmetric situations' I mean those situations where electric field is known to be a constant on the entire surface where integration is being performed. Since E is a constant therefore it can be taken out of the integral sign and dA could be integrated and then E can be found.
This method has very powerful applications as will be discussed soon.
COULOMB'S LAW IS CONTAINED IN GAUSS' THEOREM
This is not the correct time for me to dwell into Maxwell's equations but one or two words maybe useful. The four Maxwell equations contain the whole theory of electromagnetism! Yes that's not a misprint. The four Maxwell equations really contain the whole theory of electromagnetism. Physics students wear T - shirts which have these equations printed on them.
If you happen to take a look at Maxwell's equations of electromagnetism you'll find that they do not contain Coulomb's law. How can that be?
Coulomb's law is surely a very important basic principle of electromagnetism.
The answer is because its already contained in Gauss' theorem. Here's the proof.
|
|
For a brilliant discussion of Electrostatics and other such topics of Physics I recommend "Fundamentals of Physics" by Resnick, Walker and Halliday.
You may buy it by clicking on the link to the left. |