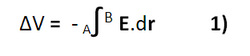ELECTRIC POTENTIAL AND POTENTIAL ENERGY
ELECTRIC POTENTIAL
Undoubtedly the concepts of electric field and electric field lines play an important role in the development of electromagnetism but no matter how useful it is electric field is at last a vector quantity. Obviously it is much easier to deal with scalars than with vectors. Physicists needed a way to deal with electromagnetic situations without needing to go in vectors. Then the concept of electric potential was born.
Electric potential is a scalar quantity, a specific number that is assigned to every point of the region containing the electric field. Obviously this number is chosen with some rules.
Since the particle is taken from one point to another therefore only the difference between the two numbers is important. For mathematical convenience potential at infinity is taken to be zero. With this setting potential at a point can be defined as follows.
DEFINITION OF ELECTRIC POTENTIAL AND POTENTIAL DIFFERENCE
Take a positive charge of any magnitude. You (or any other external agent for that sake) bring it from infinity - infinity here implies a region where electric field is zero - to the point whose electric potential is required in such a way that the charge moves with the minimum possible velocity i.e the velocity should tend to zero. (This 'tending to zero' condition can also be stated by saying that one should calculate the minimum work done by the external agent.) Calculate your work done in this process. Divide the work by the magnitude of charge. The result that you get is the electric potential of the point in question.
OR
The minimum work done by an external agent in bringing a unit positive charge from infinity to a particular point is numerically equal to the electric potential of that point.
OR
The negative of the work done by the internal conservative forces in bringing a unit positive charge from infinity to a particular point is numerically equal to the electric potential of that point.
It will be shown later on in this article that the potential difference ΔV between the two points A and B in an electric field is given by
You must note that
the minimum work done by an external agent = negative of the work done by internal conservative forces.
You should be able to see that all the above three definitions are different aspects of the same thing.
Potential is usually denoted by the letter V.
The above definitions ensure that a unique number is assigned to any point in space i.e the same point cannot have two numbers. (Can you see why?) Obviously this should be the case if the concept of electric potential has to have a logical meaning.
Since work can be positive or negative therefore electric potential can also be positive and negative . It can be seen from the definition of electric potential that positive charge will produce a positive potential and negative charge will produce a negative potential.
Note: If nothing is mentioned then by 'potential' I'll mean 'electrical potential'.
Since potential = (Work) / (Charge) therefore its unit is Joule/ Coulomb which is named as Volt.
Different charge configurations will generate different potentials. Mathematically speaking the potential function V(r) of a charge configuration at a distance r from the origin will be different for different charge configurations.
For a point charge q the potential V(r) is given by
V(r) = (1/4πЄo) (q/r). 2)
The proof is provided below after explaining the electric potential energy.
the minimum work done by an external agent = negative of the work done by internal conservative forces.
You should be able to see that all the above three definitions are different aspects of the same thing.
Potential is usually denoted by the letter V.
The above definitions ensure that a unique number is assigned to any point in space i.e the same point cannot have two numbers. (Can you see why?) Obviously this should be the case if the concept of electric potential has to have a logical meaning.
Since work can be positive or negative therefore electric potential can also be positive and negative . It can be seen from the definition of electric potential that positive charge will produce a positive potential and negative charge will produce a negative potential.
Note: If nothing is mentioned then by 'potential' I'll mean 'electrical potential'.
Since potential = (Work) / (Charge) therefore its unit is Joule/ Coulomb which is named as Volt.
Different charge configurations will generate different potentials. Mathematically speaking the potential function V(r) of a charge configuration at a distance r from the origin will be different for different charge configurations.
For a point charge q the potential V(r) is given by
V(r) = (1/4πЄo) (q/r). 2)
The proof is provided below after explaining the electric potential energy.
ELECTRIC POTENTIAL ENERGY
Throw a positive charge with an initial speed v towards another fixed positive charge in a frictionless and resistance less environment. One will find that the speed of the first charge goes on decreasing continuously as it keeps on approaching the target and eventually it becomes stationary. Let's say that the position where it stops is P. Then it reverses its direction and retraces its path.
Well here we are not interested in the entire trajectory of the particle. Let's concentrate on the point P.
The charged particle initially had a speed v which means it had some kinetic energy. At P its speed became zero so its kinetic energy too became zero. There are no resistive forces present. So where did this energy go?
According to the hypothesis of conservation of energy, energy can neither be created nor be destroyed. So the lost kinetic energy must appear in some other form. This form (in our example) is the electrical potential energy.
Some of my students have objected that here physicists have artificially invented a new kind of energy just to save their energy conservation law. It maybe that the rule of conservation of energy fails here.
Well for such skeptics I have the following reply. The charge does not becomes stationary forever. It is in rest momentarily at P. Then it starts to move in the opposite direction with increasing velocity or in other words its kinetic energy goes on increasing this time. I want to ask such skeptics that from where is this kinetic energy coming?
The answer is now the stored electrical potential energy of the system is being converted into the kinetic energy of the charged particle as the kinetic energy of the incident particle was being converted into the potential energy of the system when it was moving towards the target.
Until now you must have got a qualitative 'feel' of electrical potential energy. Now let's put it in quantitative form.
DEFINITION OF CHANGE IN POTENTIAL ENERGY AND POTENTIAL ENERGY
The negative of the work done by internal conservative forces is defined as the change in potential energy of the system. If the potential energy in one configuration of the system is defined then - and only then - the potential energy of some other configuration can be defined.
The most widely accepted notion of defining potential energy is as follows.
When all the parts of the system are at an infinite distance from each other then the potential energy of the system is taken to be zero. With this setting the definition of potential energy becomes:
The minimum work required by an external agent in assembling a system by bringing in its each part from infinity is known as the potential energy of the system.
Potential energy is usually denoted by the symbol U.
You should remember the previous definition and equation as you remember 2 + 2 = 4.
The three words written in bold above need some more explanation.
internal - you only have to take the forces of the system. Don't include external forces.
change - only changes in potential energy can be measured and have a meaning. You cannot speak of the potential energy itself until you arbitrarily define the potential energy at some point to have some specific value.
system - potential energy is defined only for a system. You cannot speak of potential energy of (say) a single isolated charged particle.
Since electric potential energy is a form of energy hence its unit is joule.
Note that electric potential energy and electric potential are two entirely different concepts. The two terms are quite similar to each other and hence this may result in a lot of confusion if one is not careful.
The work done in bringing a unit charge from infinity to a particular point is V (numerically). Therefore the work done in bringing a charge q from infinity to a particular point should be qV. But by definition this work is the potential energy U. Therefore
U = q V
For two point charges the system's potential energy is given by
U = (1/4πЄo) (q1q2/r) 3)
The proof of this equation and equation 2 is provided below.
PROOFS OF EQUATIONS 2 AND 3
It is strongly recommended that before proceeding on with the following proof you must read my blog post on the
work done by a variable force.
THE RELATION BETWEEN ELECTRIC FIELD INTENSITY AND ELECTRIC POTENTIAL
Now I prove a very important and widely used equation of electrostatics. It establishes the relation between electric field intensity and electric potential.
Let a charge q be taken from the point A to the point B in an electric field.
By definition of change in potential energy I get
This is the relationship between electric field intensity at a point and the change in potential in undergoing a displacement dr. Equation 4 can be used to find V when E is known or E when V is known.
Next article is about Gauss' Theorem.
Next article is about Gauss' Theorem.
|
|
For a brilliant discussion of Electrostatics and other such topics of Physics I recommend "Fundamentals of Physics" by Resnick, Walker and Halliday.
You may buy it by clicking on the link to the left. |